1. 標準偏差とは
Excel を使えば簡単! 標準偏差を利用してばらつきを分析してみよう
2022 年 1 月 19 日
Microsoft Excel でデータ分布のばらつきを知りたいときに役立つ標準偏差。集団の特性を見極める際の材料となる平均値と同様に、データを多角的に把握するための重要な材料となります。
この記事では偏差値を求める際に利用する関数の使い方や、図の生成方法について解説します。
標準偏差とは、データ分布の広がり (ばらつき) を示す物差しの 1 つのことです。
平均からどれだけのブレがあるかを数値で表現することができます。
たとえば、サイズが 1m の製品を A 工場と B 工場で 10 個ずつ製作した場合、どちらも平均は 1m だったとします。
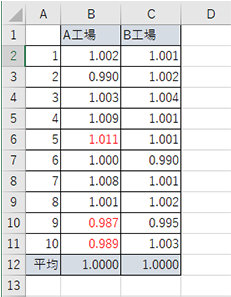
しかし、仮に 1cm 以内の誤差が許容範囲である場合、A 工場では 3 つも不合格製品が出てしまったのに対し、B 工場が作った製品はすべて合格だったことになります。この場合、A 工場では品質の改善を行う必要がありますし、B 工場で製作した製品のほうが安定した品質であるということがいえます。
あるいは、売上拡大を目指している飲食チェーン店において、客単価が平均 3,000 円の A 店舗と B 店舗があったとします。
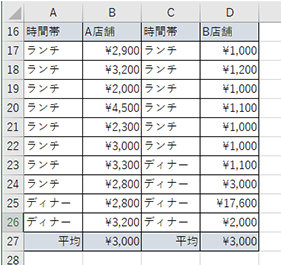
平均値は同じでも、昼の来店客数が多く客単価が高い A 店舗と、昼の来店客数は少なめで客単価も安く、夜は比較的客単価が高いB 店舗とでは、取るべき施策や行うべき分析も異なってきます。
さらに別の例を見てみましょう。
満点が 100 点となる製品アンケートを 100 人に実施した際、70 点が平均値だったとします。しかし、100 人中 100 人が 70 点を付けたのか、50 人が 90 点、残りの 50 人が50点なのかで対策が異なります。
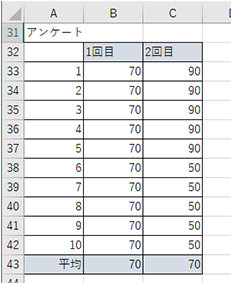
100 人が 70 点を付けた場合は、製品自体の品質の向上が必要かもしれませんし、50 人が 90 点、残りの 50 人が 50 点を付けた場合は、50 点を付けた人に 90 点を付けてもらうためにはどうするのかを検討する必要があるでしょう。
このように、平均値だけでは判断できないデータのばらつきがある場合、標準偏差と平均値を用いることによって、データがどの範囲にどのような割合で散らばっているかを明らかにすることができるのです。
2. 標準偏差を利用する関数
標準偏差では、数値が大きいとばらつきが大きく、小さいとばらつきが小さいと捉えます。
標準偏差を算出する際は、複雑な計算が必要となるため手入力で行うのは困難ですが、Excel では関数を用いることで簡単に標準偏差を確認できます。
2-1. STDEV.P
母集団の総量に対するばらつきを求める場合は、STDEV.P 関数を用います。工業製品では全量のクオリティ チェックを行うケースがありますが、こういった製品の全量に対するばらつきを確認する場合に利用します。
STDEV.P 関数は以下の式を使い、標準偏差の元となる値をかっこ内の引数に指定し使用します。
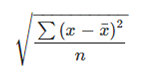
それでは先ほどの工場の例を用いて、標準偏差の値を求めてみましょう。
STDEV.P 関数を用いた標準偏差
1. 標準偏差を表示したいセルを選択し、「=STDEV.P(」を入力する
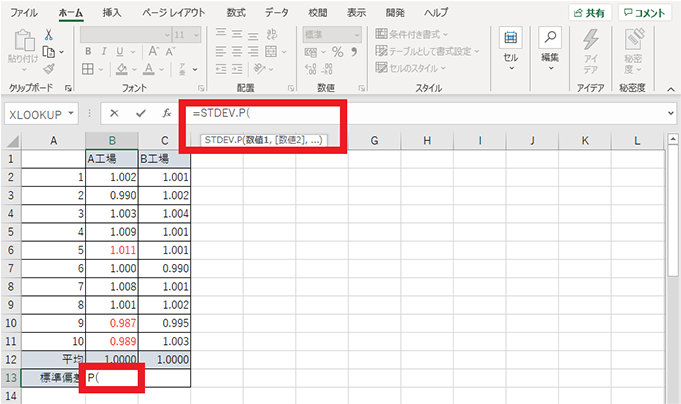
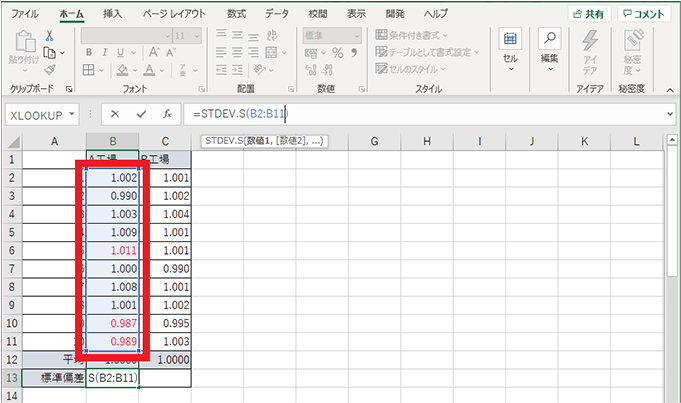
2. 引数を指定する (例では B2 から B11)
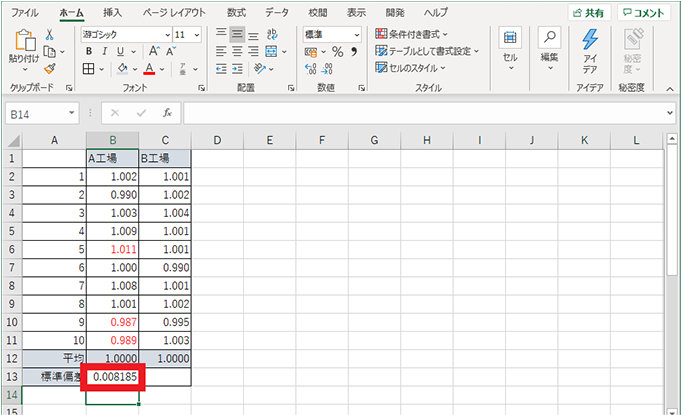
3. 標準偏差が算出される
4. 同様に 1～3 の操作を行い、B 工場の標準偏差を算出する
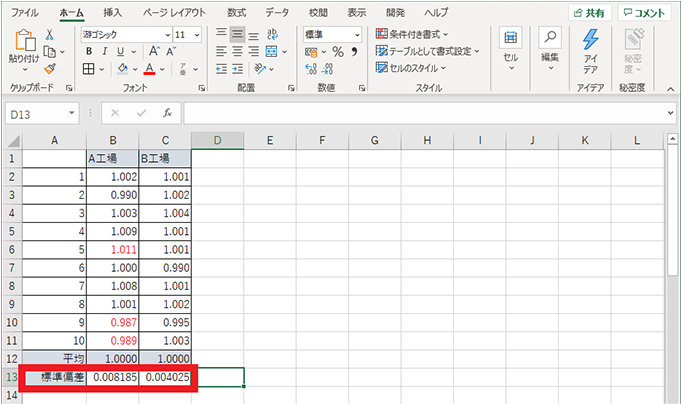
標準偏差で見ると、A 工場の数値が大きく、ばらつきが大きいことが分かりました。
2-2. STDEV.S
全数ではなく無作為に選びだした対象から母集団のばらつきを求めたい場合は、STDEV.S を用います。母集団すべてを調べられない場合、母集団の標準偏差は分からないため、標本の標準偏差から母集団の標準偏差を推定します。
たとえば、大豆の品質のばらつきを確認する場合、すべての豆をチェックせず、ロットの一部などを抽出して全体を推計することになります。そういった場合に利用するのが、この STDEV.S 関数です。
「全体から無作為に抽出する」部分にばらつきが発生するため、その補正を行った関数と考えればよく、引数を母集団の標本であると見なします。
この関数は統計学としては標本標準偏差、つまり母集団を元にした標準偏差ではなく、不偏分散の平方根としての標準偏差、つまりサンプルを抽出した場合の値となるため、同じ値を算出した場合 STDEV.P の値より値が大きくなることに注意が必要です。
STDEV.S 関数は以下の式を使い、標準偏差の元となる選び出した値をかっこ内の引数に指定し使用します。
それでは、先ほどの工場の例が抜き取りで検査された製品の大きさだと仮定し、標準偏差の値を求めてみましょう。
STDEV.S 関数を用いた標準偏差
1. 標準偏差を表示したいセルを選択し、「=STDEV.S(」を入力する
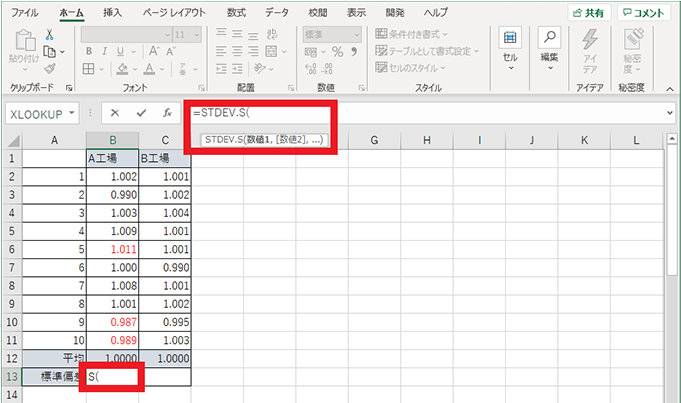
2. 引数を指定する (例では B2 から B11)
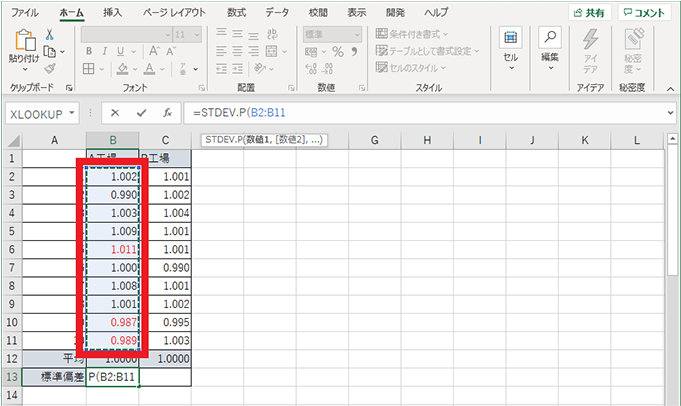
3. 標準偏差が算出される
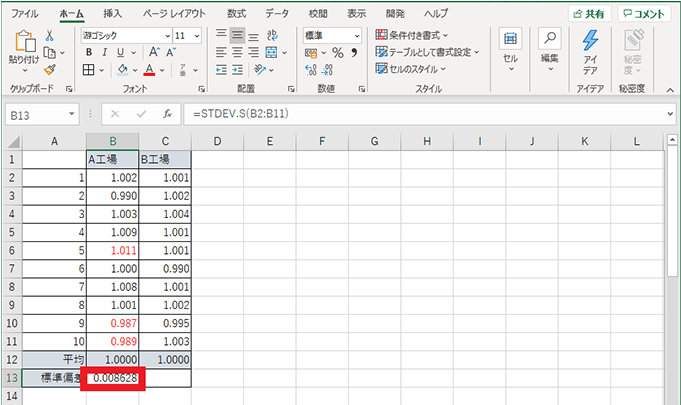
4. 同様に 1～3 の操作を行い、B 工場の標準偏差を算出する
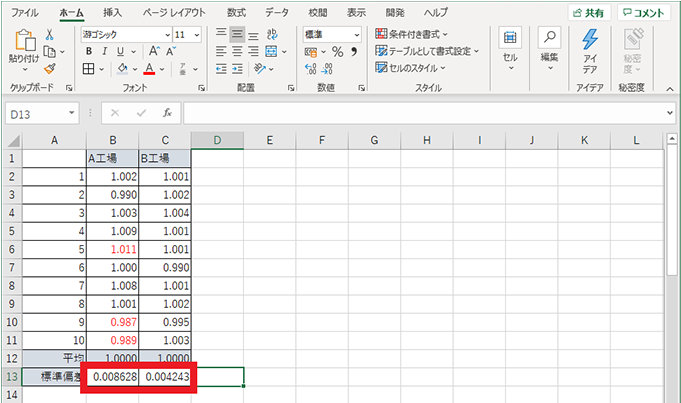
STDEV.S 関数を用いた標準偏差で見ても、A 工場の数値が大きく、ばらつきが大きいことが分かりました。
3. 標準偏差を利用したグラフの作成
前段で標準偏差を利用するケースを解説しましたが、実際はこの数値を見ただけでは直感的に理解するのは難しいかもしれません。
そこで次に、標準偏差を図に起こして可視化する方法について解説します。ここでも工場の製品を例に見ていきましょう。
3-1. 散布図
散布図は値が 2 つの方向軸のどこに位置するのかを図示するものです。
これを利用することで、データのばらつきを可視化することができます。
以下の図は、先ほどの A 工場と B 工場の製品の大きさのデータを Excel の散布図にしたものです。A 工場の製品は 1.000 付近のデータだけでなく、1.000 から外れた 1.010 や 0.990 付近にもデータが散在していますが、B 工場の製品の多くは 1.000 付近にデータが集中していることが分かります。
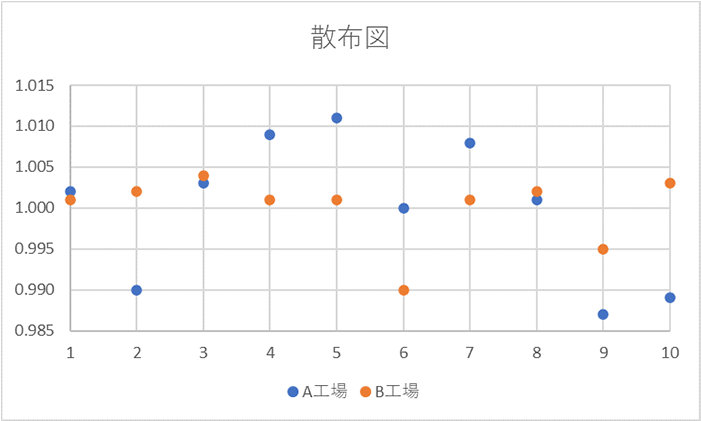
3-2. 棒グラフ
平均値に標準誤差のエラー バーを付けることで、誤差を可視化することができます。標準誤差とは、標準偏差÷データの個数の平方根で求められ、推定値にどれくらいばらつきがあるものなのかを示します。
元のデータのバラツキ具合 (＝標準偏差) が大きければ標準誤差も大きくなり、標本数が少なければ分母が小さくなるため、標準誤差が大きくなります。
エラー バーは特定の値からどの程度のばらつきがあるかをグラフ内で表します。母集団全体の分布を表現したい場合は標準偏差を用いますが、平均値などの推定値の分布を表現したい場合は標準誤差を利用します。
標準誤差は、標準偏差を求める STDEV 関数、平方根を求める SQRT 関数、数値の件数を求める COUNT 関数を用いて算出し、エラー バーとして付与します。
今回は、A 工場の製品を抜き取りで検査したとして、平均値のばらつきがどう変化していったのかを棒グラフで可視化してみましょう。
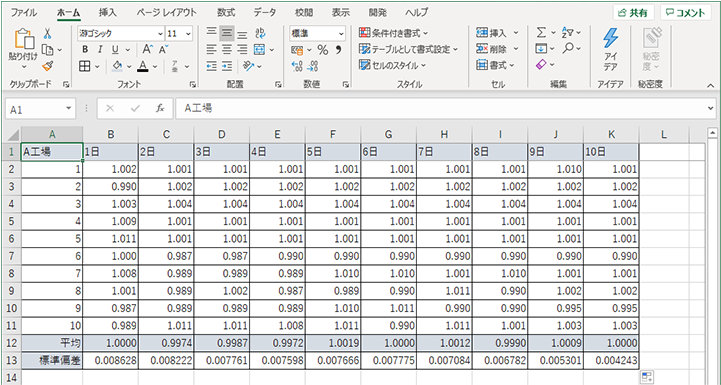
標準誤差のエラー バー付き棒グラフの作成
1. グラフ用に標準誤差の行を追加する
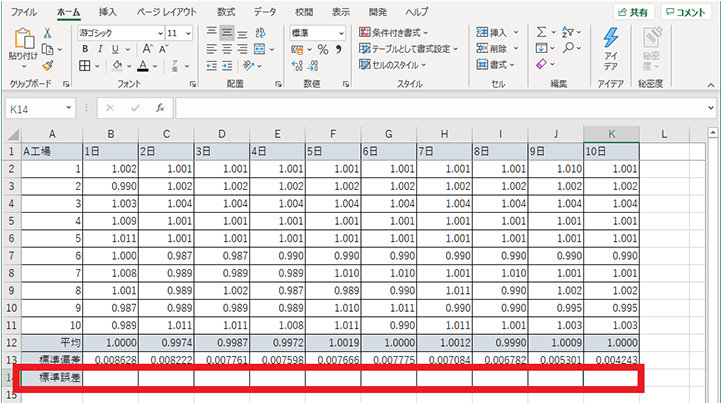
2. 1 日の列に標準誤差を求めるための数式「=STDEV.S/SQRT(COUNT)」を入力する (例では「=STDEV.S(B2:B11)/SQRT(COUNT(B2:B11))」)
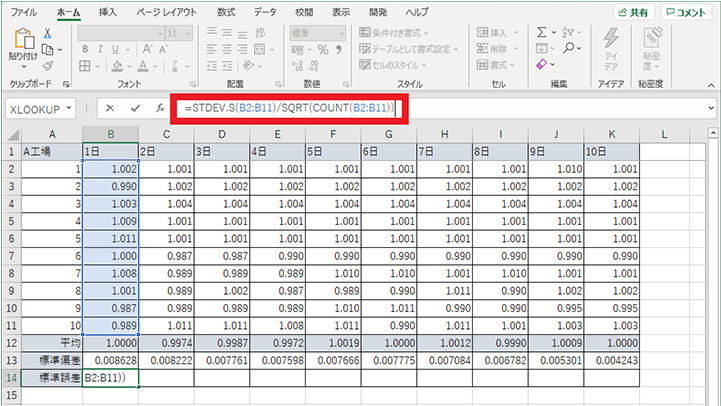
3. 2 日～10 日にも標準誤差の式を設定する
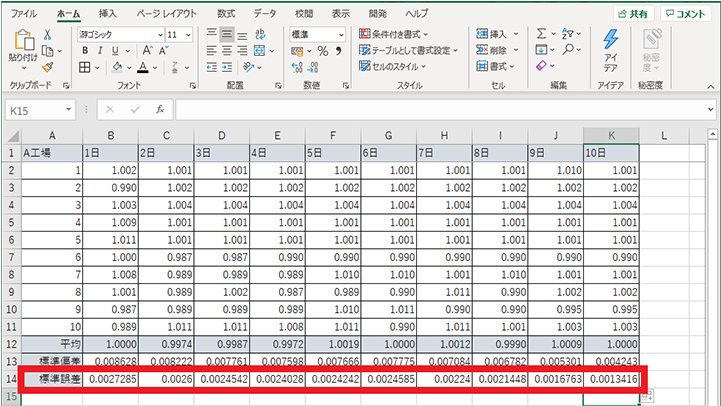
4. 日付と平均のセルを選択する
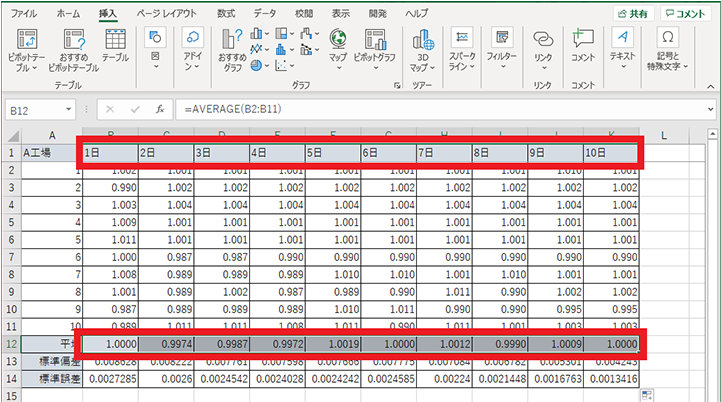
5. 挿入タブの棒グラフから積み上げ縦棒をクリックする
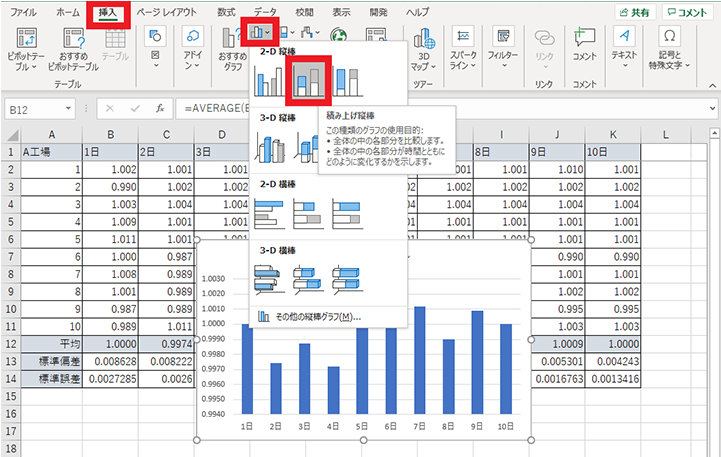
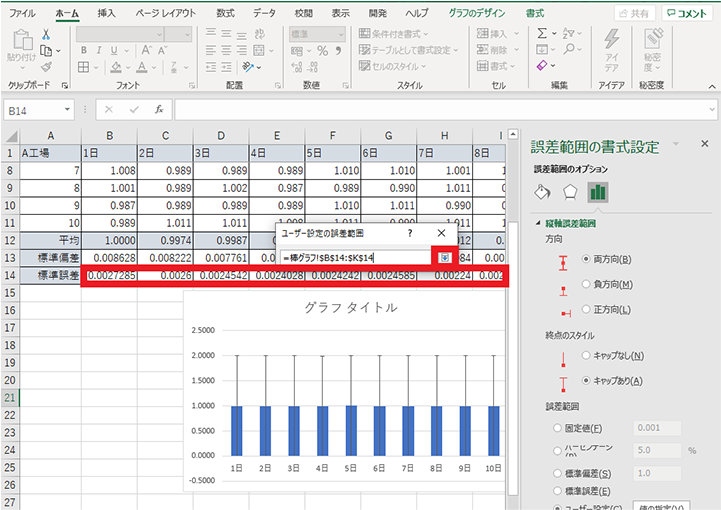
6. グラフを選択した状態で、グラフのデザイン タブからグラフ要素を追加、誤差範囲、その他の誤差範囲オプションをクリックする
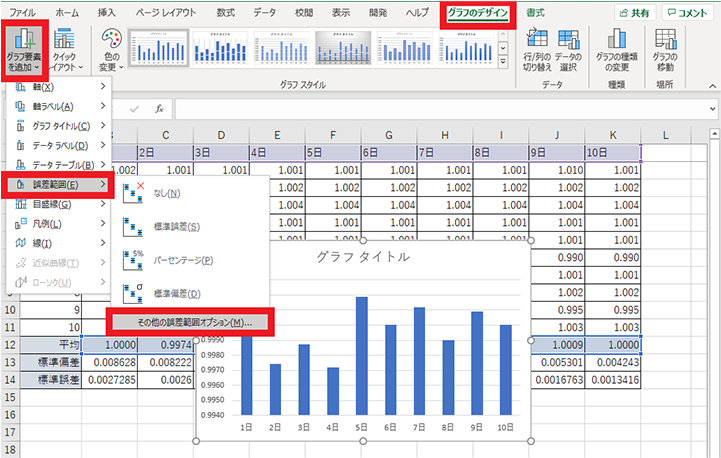
7. 誤差範囲を表す黒い線をクリックする
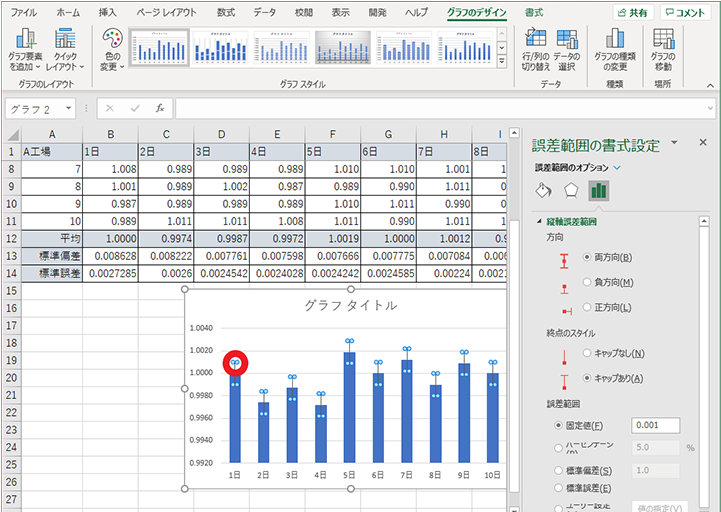
8. 誤差範囲の書式設定で、縦軸誤差範囲の中の誤差範囲欄でユーザー設定をクリックし、「値の指定」ボタンをクリックする
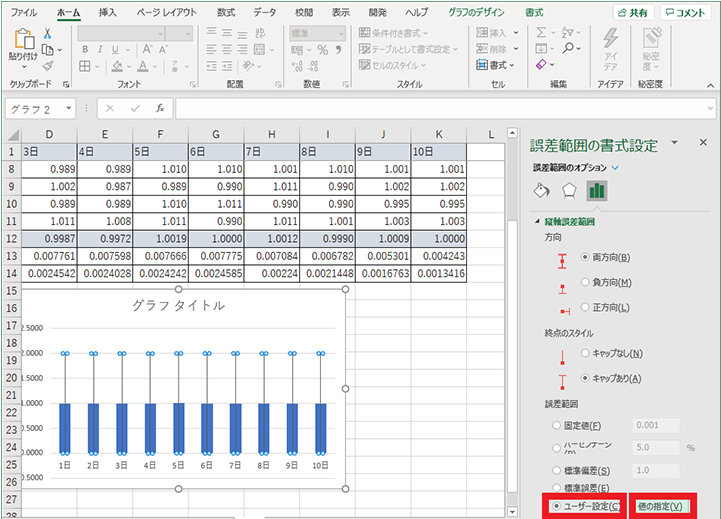
9. ユーザー設定の誤差範囲画面が表示されるので、正の誤差の値の「↑」ボタンをクリックする
10. 先ほど作成した標準誤差のセルを選択し、「↓」ボタンをクリックする
11. 同様に 9～10 の手順で負の誤差の値を設定し、「OK」ボタンをクリックする
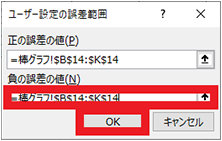
12. 標準誤差のエラー バー付き棒グラフが作成される
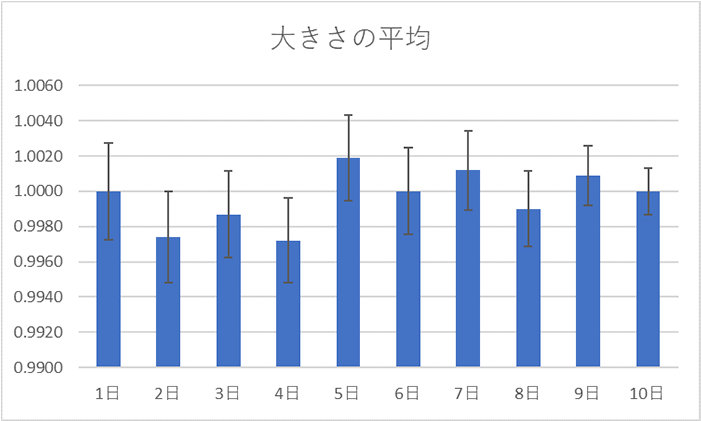
グラフにエラー バーが付き、ばらつきが可視化されました。
3-3. 正規分布曲線
平均値を中央にして、標準偏差に従い正規化された形で分布を見るものを正規分布曲線といいます。
標準偏差で出力される値を「σ」 (シグマ) で表した場合、1σ には約 68%、2σ には約 95%、3σ には約 99% のデータが含まれていると考えるものが正規分布です。
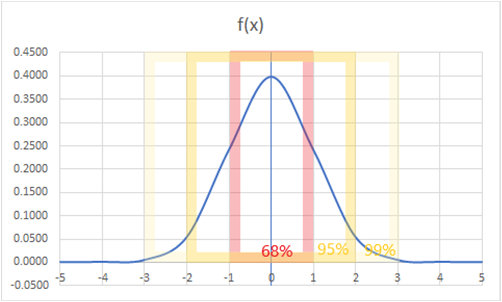
規分布では多数のデータがあればその値に収束するものと考えます。
実際の値と比較することでとびぬけて量が多い場合などは、何らかの問題が発生しているものと考えられるため、集団の傾向を測るのに適しています。
正規分布曲線は、正規分布の値を返す NORM.DIST 関数を用いて算出します。
ここでは、B 工場の製品の平均値と標準偏差を例に、正規分布曲線を作成してみましょう。
正規分布曲線の作成
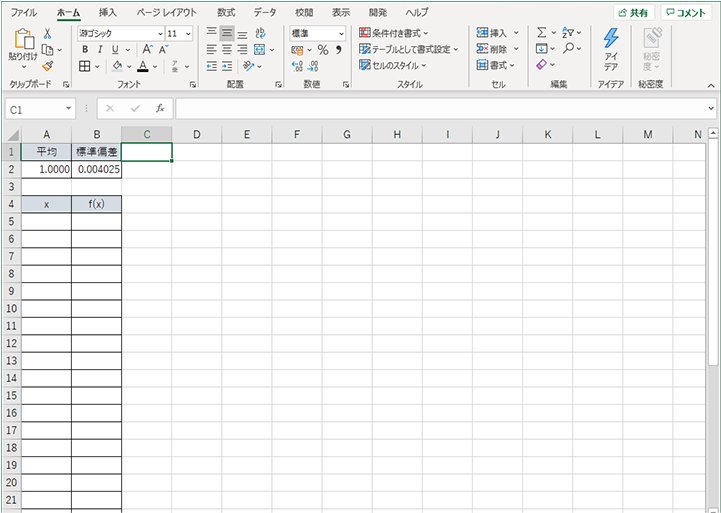
1. 正規分布曲線を作成するためのデータを用意するため、B 工場の製品の平均値と標準偏差を入力し、確率変数 x、正規分布の値 f(x) の枠を作成する (例では x は製品の大きさ)
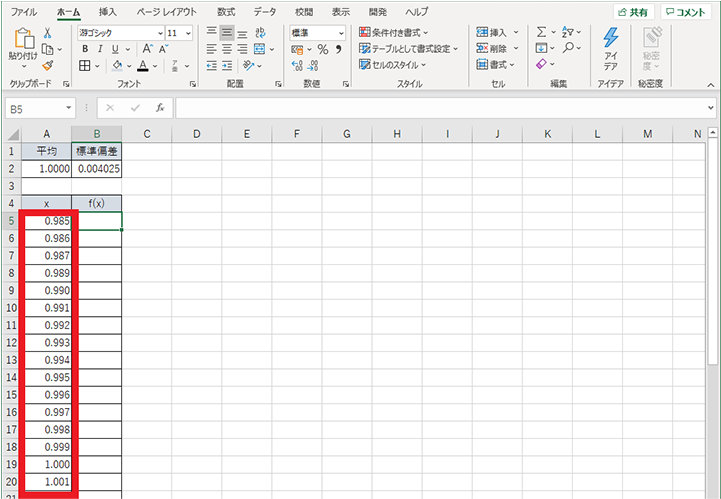
2. x に 0.985 から 1.015 まで、0.001 刻みで数値を入力する
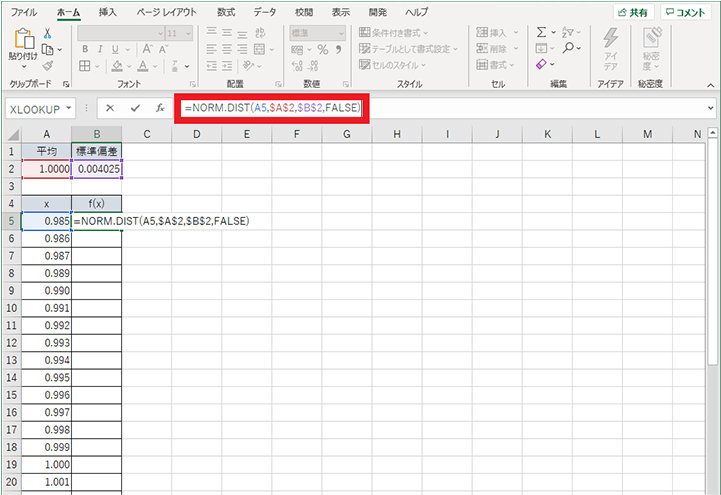
3. f(x) の列に正規分布の値を求めるための数式「=NORM.DIST()」を入力する (例では「=NORM.DIST(A5,$A$2,$B$2,FALSE)」)
4. f(x) の列に数式をコピー & ペーストし、データを作成する
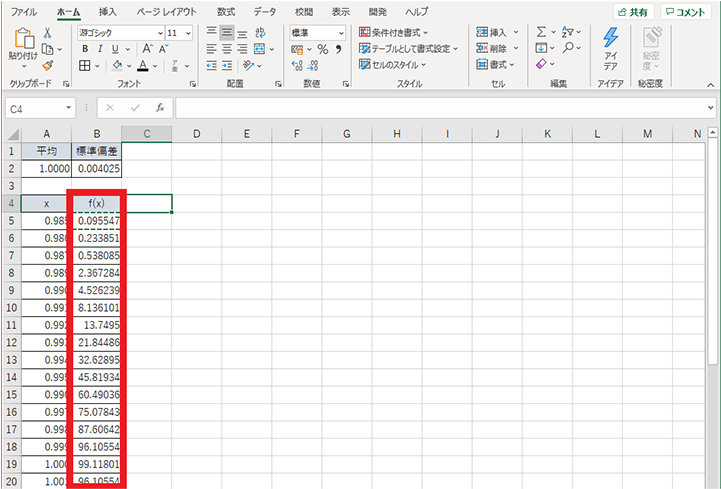
5. x と f(x) の値を選択する
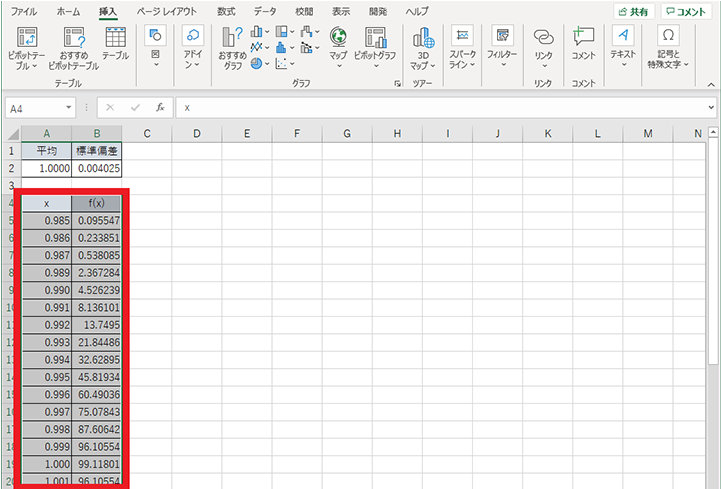
6. 挿入タブの散布図から散布図 (平滑線) をクリックする
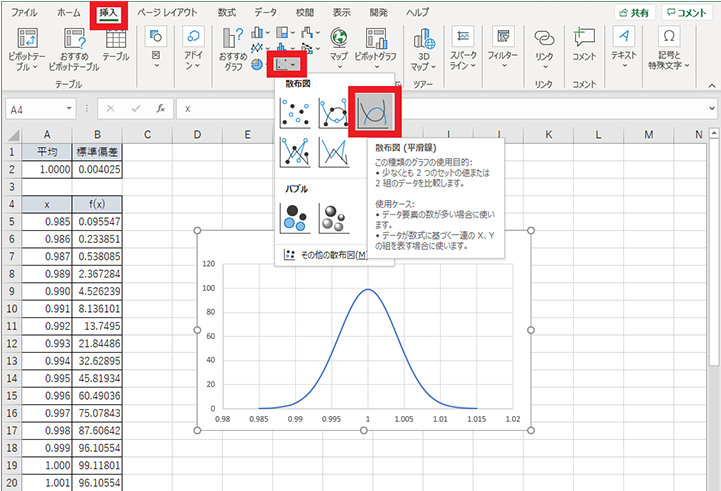
7. 正規分布曲線が作成される
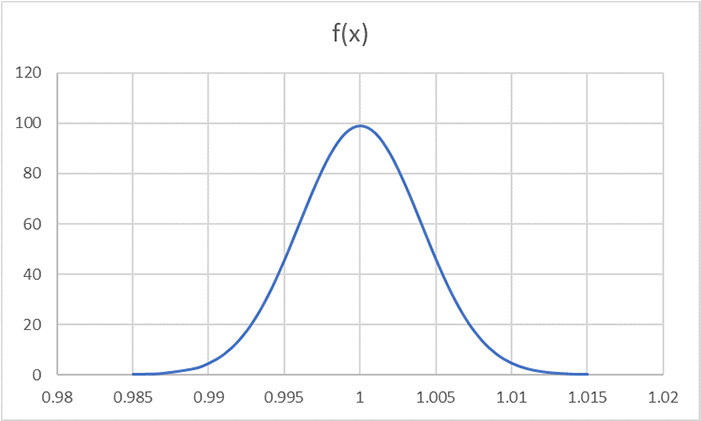
平均 1m、標準偏差 0.004025 なので、1±0.004025 の間に全体の約 68%、1±2×0.004025 の間に全体の約 95%、1±3×0.004025 の間に全体の約 99% のデータが含まれることになります。この曲線から外れるデータ、たとえば 100 個の製品を製造して、3σ の値よりも大きい 1.013m の製品が 2 個以上製造されたり、2σ の範囲に該当する 0.99195m ～ 1.00805m の製品が 93 個以下で製造されたりした場合は、製造に問題があることを疑った方がよいでしょう。
4. まとめ
Excel は本来計算を面で行うための表計算ソフトです。特に複雑な計算式の偏差のようなばらつきを関数で計算し情報として整理することは、まさに Excel 本来の利用方法といえます。
Excel の機能を最大限活用し、日々の業務に役立てましょう。
【参考】関連する関数
- STDEV …標準偏差を求める
- SQRT …平方根を求める
- COUNT …数値の件数を求める
- NORM.DIST …正規分布を求める
リモートワーク・ハイブリッドワークに適した環境設置のために
リモートワーク・テレワーク・在宅勤務環境を安全・快適に実現するためには、「セキュリティの確保」「Web 会議のためのデバイス選択」「グループワークのためのアプリケーション」など検討する課題も多く、またこれらを潤沢な資金で準備するのではなくコスト削減につなげることが大切です。
これらの達成のための Microsoft 365、Excel の使い方や、リモートワーク・ハイブリッドワーク環境を充実させるために以下の記事が参考になります。
他にも Excel 作業を高速化するテクニックを厳選! 無料ガイドブック
Excel ショートカット 30 選
Microsoft 公式の超時短仕事術 Excel ショートカット 30 選です。
もっと PC スキルを学びたい、より効率的に業務を行いたいという方におすすめです。
ご購入検討の問い合わせ先
Web フォームで購入相談
本情報の内容 (添付文書、リンク先などを含む) は、作成日時点でのものであり、予告なく変更される場合があります。